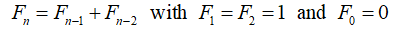The Fascinating Mathematical Beauty Of The Fibonacci Numbers
Abstract
The Fibonacci numbers are sequences of numbers of the form: 0,1,1,2,3,5,8,13,... Among numerical sequences, the Fibonacci numbers Fn have achieved a kind of celebrity status. These numbers are famous for possessing wonderful and amazing properties. Mathematicians have been fascinated for centuries by the properties and patterns of Fibonacci numbers. In mathematical terms, it is defined by the following recurrence relation:
The first number of the sequence is 0, the second number is 1, and each subsequent number is equal to the sum of the previous two numbers of the sequence itself. That is, after two starting values, each number is the sum of the two preceding numbers. In this paper, we give excellent summary of basic properties of Fibonacci numbers as well as and its patterns. This is a paper which is very helpful for quick reference on Fibonacci numbers.
Downloads
References
http://jwilson.coe.uga.edu/emt669/Student.Folders/Morris.Stephanie/EMT.669/Essay.3/Fibonacci.Essay.html
Knott R, Quinney D A and PASS Maths, ,”The life and numbers of Fibonacci”, 1997
“Fibonacci Number”. Wolfram MathWorld. the web’s most extensive mathematics resource http://mathworld.wolfram.com/FibonacciNumber.html
Spencer D, Invitation To The Number Theory With Pascals.
Burton, D. M., Elementary number theory. New York City, New York: McGraw-Hill. 1998.
Koshy T., Fibonacci and Lucas Numbers with Applications, New York City, New York: John Wiley and Sons, Inc. 2001.
Copyright (c) 2021 GPH - International Journal of Mathematics

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Author(s) and co-author(s) jointly and severally represent and warrant that the Article is original with the author(s) and does not infringe any copyright or violate any other right of any third parties, and that the Article has not been published elsewhere. Author(s) agree to the terms that the GPH Journal will have the full right to remove the published article on any misconduct found in the published article.